Aprendendo Matemática
História da Matemática
História da Matemática
Introdução
A matemática é a ciência dos números e dos cálculos. Desde a antiguidade, o homem utiliza a matemática para facilitar a vida e organizar a sociedade. A matemática foi usada pelos egípcios nas construções de pirâmides, diques, canais de irrigação e estudos de astronomia. Os gregos antigos também desenvolveram vários conceitos matemáticos. Atualmente, esta ciência está presente em várias áreas da sociedade como, por exemplo, arquitetura, informática, medicina, física, química etc. Podemos dizer que em tudo que olhamos existe a matemática.
Abaixo, um pequeno histórico da evolução histórica da matemática:
4000 a.C. - Na Mesopotâmia, os sumérios desenvolvem um dos primeiros sistemas numéricos, composto de 60 símbolos.
520 a.C. - O matemático grego Eudoxo de Cnido define e explica os números irracionais.
300 a.C. - Euclídes desenvolve teoremas e sintetiza diversos conhecimentos sobre geometria. É o início da Geometria Euclidiana.
250 - Diofante estuda e desenvolve diversos conceitos sobre álgebra.
500 - Surte na Índia um símbolo para especificar o algarismo zero.
1202 - Na Itália, o matemático Leonardo Fibonacci começa a utilizar os algarismo arábicos.
1551 - Aparece o estudo da trigonometria, facilitando em pleno Renascimento Científico, o estudo dos astros.
1591 - O francês François Viète começa a representar as equações matemáticas, utilizando letras do alfabeto.
1614 - O escocês John Napier publica a primeira tábua de algorítimos.
1637 - O filósofo, físico e matemático francês René Descartes desenvolve uma nova disciplina matemática: a geometria analítica, com a misitura de álgebra e geometria.
1654 - Os matemáticos franceses Pierre de Fermat e Blaise Pascal desenvolvem estudos sobre o cálculo de probabilidade.
1669 - O físico e matemático inglês Isaac Newton desenvolve o cálculo diferencial e integral.
1685 - O inglês John Wallis cria os números imaginários.
1744 - O suíço Leonard Euler desenvolve estudos sobre os números transcendentais.
1822 - A criação da geometria projetiva é desenvolvida pelo francês Jean Victor Poncelet.
1824 - O norueguês Niels Henrik Abel conclui que é impossível resolver as equações de quinto grau.
1826 - O matemático russo Nicolai Ivanovich Lobachevsky desenvolve a geometria não euclidiana.
1931 - Kurt Gödel, matemático alemão, comprova que em sistemas matemáticos existem teoremas que não podem ser provados nem desmentidos.
1977 - O matemático norte-americano Robert Stetson Shaw faz estudos e desenvolve conhecimentos sobre A Teoria do Caos.
1993 - O matemático inglês Andrew Wiles consegue provar através de pesquisas e estudos o último teorema de Fermat.
Principais áreas da Matemática:
- Aritmética
- Álgebra
- Geometria
- Geometria Analítica
- Porcentagem
- Trigonometria
- Estatística
- Educação Matemática
sexta-feira, 14 de junho de 2013
Racionalização
 o denominador
o denominador  é um número irracional e deve ser eliminado.
é um número irracional e deve ser eliminado.Atenção: o importante é eliminar a raiz (que pode ser quadrada, cúbica, etc), mantendo uma fração "equivalente", ou seja, que representa o mesmo valor.
Uma dica é multiplicar tanto o numerador (parte de cima), quanto o denominador pelo mesmo número, o que não interfere na igualdade. Se a fração anterior for multiplicada em cima e em baixo por
 ficará:
ficará: . Note que
. Note que  é igual a 1, logo a multiplicação de um número por 1 não o altera.
é igual a 1, logo a multiplicação de um número por 1 não o altera.Prosseguindo:
 |
Como se pode notar o denominador agora é um número racional (3).
Raízes não quadradas
Para eliminar raízes cúbicas, ou de outros índices diferentes de 2 (lembre-se: raiz quadrada é, na verdade, uma raiz de índice 2!), é necessário utilizar um artifício.
 |
Multiplique, no numerador e no denominador, por uma raiz de mesmo radicando (o número dentro da raiz) e cujo índice seja equivalente ao índice da raiz original menos um. Por exemplo:
 |
Soma de raízes no denominador
Veja:
 |
Deve-se multiplicar por
 .
.Isso porque a multiplicação de
 por
por  é, na verdade, a multiplicação de (a + b). (a - b), um produto notável, cujo resultado é (a2 - b2) - isto é, os radicais somem!
é, na verdade, a multiplicação de (a + b). (a - b), um produto notável, cujo resultado é (a2 - b2) - isto é, os radicais somem!
 |

Operações com radicais
1º CASO : Os radicais não são semelhantes
Devemos proceder do seguinte modo:
a) Extrair as raízes (exatas ou aproximadas)
b) Somar ou subtrair os resultados
Exemplos
1) √16 + √9 = 4 + 3 = 7
2) √49 - √25 = 7 – 5 = 2
3) √2 + √3 = 1,41 + 1,73 = 3,14
Neste último exemplo, o resultado obtido é aproximado, pois √2 e √3 são números irracionais (representação decimal infinita e não periódica)
2º CASO: Os radicais são semelhantes.
Para adicionar ou subtrair radicais semelhantes, procedemos como na redução de termos semelhantes de uma soma algébrica.
Exemplos:
a) 5√2 + 3√2 = (5+3)√2 = 8√2
b) 6³√5 - 2³√5 = (6 – 2) ³√5 = 4³√5
c) 2√7 - 6√7 + √7 = (2 – 6 +1) √7 = -3√7
3º CASO: Os radicais tornam-se semelhantes depois de simplificados.
Exemplos
a)5√3 + √12
..5√3 + √2².3
..5√3 + 2√3
..7√3
b)√8 + 10√2 - √50
..√2².√2 +10√2 - √5². √2
..2√2 + 10√2 - 5√2
..7√2
MULTIPLICAÇÃO E DIVISÃO
1º Caso: Os radicais têm o mesmo índice
Efetuamos a operação entre os radicandos
Exemplos:
a) √5 . √7 = √35
b) 4√2 . 5√3 = 20√6
c) ⁴√10 : ⁴√2 = ⁴√5
d) 15√6 : 3√2 = 5√3
2º Caso: Os radicais não têm o mesmo índice
Inicialmente devemos reduzi-los ao mesmo índice
Exemplos
a) ³√2 . √5 = ⁶√2² . ⁶√5³ = ⁶√4 . ⁶√125 = ⁶√500
b)⁵√7 : √3 = ¹⁰√7² : ¹⁰√3⁵ = ¹⁰√49/243
REFERENCIA: http://ensinodematemtica.blogspot.com.br/2011/05/operacoes-com-radicais.html
Simplificação de radicais através da fatoração
Raízes
Exemplos
Nenhum valor de a negativo (-a) tem definição nesse caso.
Observação: quando o índice não aparecer no radical, isso indica que n = 2 e teremos uma raiz quadrada.
Exemplos:

Nesse caso é possível obtermos raízes negativas dentro do conjunto dos números reais (ℝ).
Exemplos:
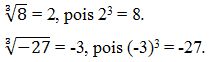
terça-feira, 11 de junho de 2013
 |
| Operações Fundamentais da Matemática |
Quantas vezes nós professores de Matemática temos que ouvir essa pergunta: "Onde vou usar isso". Existe uma certa ignorância da parte dos alunos para aprender por achar que isso será em vão, já que eles acreditam que não irão utilizar tal aprendizagem.
E daí vem a necessidade da contextualização, quando mostramos para os alunos momentos em que ele pode utilizar aquilo que aprende em sala, e ainda melhor onde ele já utiliza em seu dia a dia mas de um modo diferente, dá outra visão para o aluno, a Matemática deixa de ser abstrata torna-se algo 'apalpável' e necessário.
Por isso nós professores temos que nos esforçar cada vez mais nesse sentido, ajudando assim nossos alunos, dando para eles a visão que nós temos da Matemática, vendo-a como algo prazeroso, pois quanto mais eles entenderem mais eles irão gostar da Matemática.
TEXTO REFLEXIVO: Matemática da vida
- Somar alegrias;
- Diminuir tristezas;
- Multiplicar felicidade;
- E dividir amor.
Nestas dimensões, certamente todos gostamos da matemática.
Somar alegrias.
Quem vive sozinho, longe dos outros, sem compartilhar alegrias, sem permutar experiências, diminui sua própria alegria e não alcança a felicidade. Ficamos, às vezes, penalizados, vendo tanta gente que ainda não fez esta descoberta. Pessoas que se fecham sobre si mesmas, por medo ou egoísmo, palmilham caminhos errados. Quem teme perder sua alegria, repartindo-a com os outros, ainda não aprendeu a psicologia humana.
Diminuir tristezas
A vida tem dessas compensações gratificantes. Quando conseguimos minorar a tristeza, nós é que saímos lucrando. Uma das mais profundas satisfações reservada a um coração humano é restituir o entusiasmo, a coragem e o
otimismo aos irmãos da caminhada.
Multiplicar felicidade
Na família, no trabalho, na comunidade, em qualquer lugar onde plantamos felicidade, nós a multiplicamos. Felicidade partilhada é felicidade pessoal multiplicada.
Dividir o amor
Em matemática, quando dividimos um número pelo outro, o resultado final é sempre menor. Nas dimensões do amor humano, acontece exatamente o contrário. Dividir o amor com os outros é multiplicá-lo, é aumentá-lo. Todo aquele que divide seu amor com alguém, descobre em seguida ter multiplicado seu amor.
Somar alegrias, diminuir tristezas, multiplicar felicidade, dividir o amor: é o mais lindo programa de vida que podemos abraçar. O ser humano é comunicativo por natureza. Não aguenta viver sozinho. O individualismo é o caminho mais certo da infelicidade, para a solidão. Somar alegrias, diminuir tristezas, multiplicar felicidade e dividir amor é a rota mais segura da Alegria de Viver. São estes os misteriosos caminhos da vida.
sexta-feira, 7 de junho de 2013
Equações do 2º Grau
2x + 1 = 0, o expoente da incógnita x é igual a 1. Dessa forma, essa equação é classificada como do 1º grau.
2x² + 2x + 6 = 0, temos duas incógnitas x nessa equação, em que uma delas possui o maior expoente, determinado por 2. Essa equação é classificada como do 2º grau.
x³ – x² + 2x – 4 = 0, nesse caso temos três incógnitas x, em que o maior expoente igual a 3 determina que a equação é classificada como do 3º grau.
Cada modelo de equação possui uma forma de resolução. Trabalharemos a forma de resolução de uma equação do 2º grau, utilizando o método de Bhaskara.
Na fórmula de Bhaskara utilizaremos somente os coeficientes. Veja:
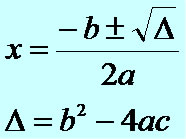
1º passo: determinar o valor do discriminante ou delta (?)
x² – 2x – 3 = 0
coeficientes: a = 1, b = –2 e c = –3.
? = b² – 4 . a . c
? = (–2)² – 4 . 1 . (–3)
? = 4 + 12
? = 16
2º passo
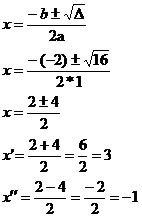
Os resultados são x’ = 3 e x” = –1.
Teorema de Pitágoras

a² + b² = c²

x² + 20² = 25²
x² + 400 = 625
x² = 625 – 400
x² = 225
√x² = √225
x = 15
Exemplo 2:
Calcule o valor do segmento desconhecido no triângulo retângulo a seguir.

x² = 9² + 12²
x² = 81 + 144
x² = 225
√x² = √225
x = 15



