Uma raiz nada mais é que uma operação inversa à potenciação, sendo
assim, ela é utilizada para representar, de maneira diferente, uma
potência com expoente fracionário.
Exemplos

Raiz com índice par
Para um número real
a positivo, com
n sendo um número natural par e positivo, maior que 1, tem-se um
b, tal que, se

=
b, então
bn = a, onde
a é o radicando,
n é o índice,
b é raiz e √ é o radical. Com
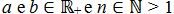
.

Raiz com índice ímpar
Sendo
a um número real, positivo ou negativo, com
m sendo um número natural ímpar e positivo, maior que 1, tem-se um
b, tal que, se

, então
bm = a, onde
a é o radicando,
m é o índice,
b é raiz e √ é o radical. Com
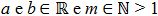
.
ℝ
).
Exemplos:
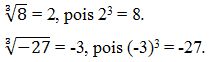

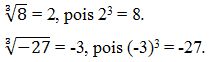
Nenhum comentário:
Postar um comentário